Mastering The LCM Of 9, 12, And 18: Your Ultimate Guide

Let’s talk about something that makes math geeks go wild: the LCM of 9, 12, and 18. Yep, you heard that right. If numbers were celebrities, the least common multiple would be the A-lister in town. But don’t let that intimidate you. Understanding LCM is like learning a secret code that unlocks a ton of math problems. So, grab a coffee (or your favorite snack), and let’s dive in!

Now, you might be wondering why we’re even talking about this. Well, here’s the deal: LCM is one of those fundamental math concepts that pops up everywhere. Whether you’re simplifying fractions, solving equations, or even planning a schedule, knowing how to calculate the LCM can save your day. And trust me, when you master it, you’ll feel like a math ninja!

So, what exactly is the LCM of 9, 12, and 18? Think of it as the smallest number that all three numbers can divide into evenly. Sounds simple, right? Well, it is—once you get the hang of it. In this article, we’ll break it down step by step, so even if math isn’t your favorite subject, you’ll leave here feeling confident and ready to tackle anything LCM-related.

• Molly Noblitt Update A Journey Through Her Life And Achievements
• Molly Noblif A Rising Star In The Entertainment Industry

Table of Contents

• What is LCM?
• Why Does LCM Matter?
• Breaking It Down: Prime Factorization
• The List Method: A Simple Approach
• Climbing the Ladder: The Ladder Method
• Real-Life Applications of LCM
• Common Mistakes to Avoid
• Tips and Tricks for Mastering LCM
• Solved Examples: Putting It All Together
• Conclusion: Your Math Journey Continues

What is LCM?

Alright, let’s start with the basics. LCM stands for Least Common Multiple. It’s like the VIP number that all the other numbers in your group can divide into without leaving any leftovers. Think of it as the ultimate meeting point for numbers. If 9, 12, and 18 are friends trying to meet up at the same spot, the LCM is the address where they all show up together.

Here’s the kicker: the LCM of 9, 12, and 18 is 36. But how do we get there? That’s what we’re about to uncover. Stick with me, and I’ll show you the ropes.

Why Do We Use LCM?

LCM isn’t just some random math concept. It’s a tool that helps us solve real-world problems. Imagine you’re planning a party and need to figure out how many snacks to buy so everyone gets an equal share. Or maybe you’re working on a project that requires coordinating schedules. LCM is your go-to solution in situations like these.

• Understanding The Molly Noblitt Punishment A Deep Dive
• Is Molly Nobbit Dead The Truth Behind The Rumors

Why Does LCM Matter?

Let’s face it: math isn’t always about abstract equations. Sometimes, it’s about making life easier. LCM is one of those tools that simplifies complex problems. For instance, if you’re dealing with fractions, finding the LCM of the denominators can make addition and subtraction a breeze.

But here’s the thing: LCM isn’t just for math nerds. It’s for anyone who wants to solve problems efficiently. Whether you’re a student, a teacher, or even a business owner, understanding LCM can save you time and effort.

Breaking It Down: Prime Factorization

Prime factorization is like the secret weapon in the world of LCM. It’s a method that breaks numbers down into their basic building blocks—prime numbers. Once you’ve got the prime factors, finding the LCM becomes a piece of cake.

Let’s take a look at our numbers: 9, 12, and 18.

• 9 = 3 × 3
• 12 = 2 × 2 × 3
• 18 = 2 × 3 × 3

Now, to find the LCM, we take the highest power of each prime number that appears in the factorization. That gives us:

• 2 × 2 × 3 × 3 = 36

And there you have it! The LCM of 9, 12, and 18 is 36.

Why Prime Factorization Works

Prime factorization works because it breaks numbers down to their simplest form. By doing this, we can easily identify the smallest number that all the original numbers can divide into. It’s like finding the common ground between them.

The List Method: A Simple Approach

If prime factorization feels a bit too complicated, don’t worry. There’s another method you can use: the list method. This one’s super straightforward. All you have to do is list the multiples of each number until you find the smallest one they all have in common.

Let’s try it with 9, 12, and 18.

• Multiples of 9: 9, 18, 27, 36, 45, …
• Multiples of 12: 12, 24, 36, 48, …
• Multiples of 18: 18, 36, 54, …

See that? The first number they all have in common is 36. Boom! There’s your LCM.

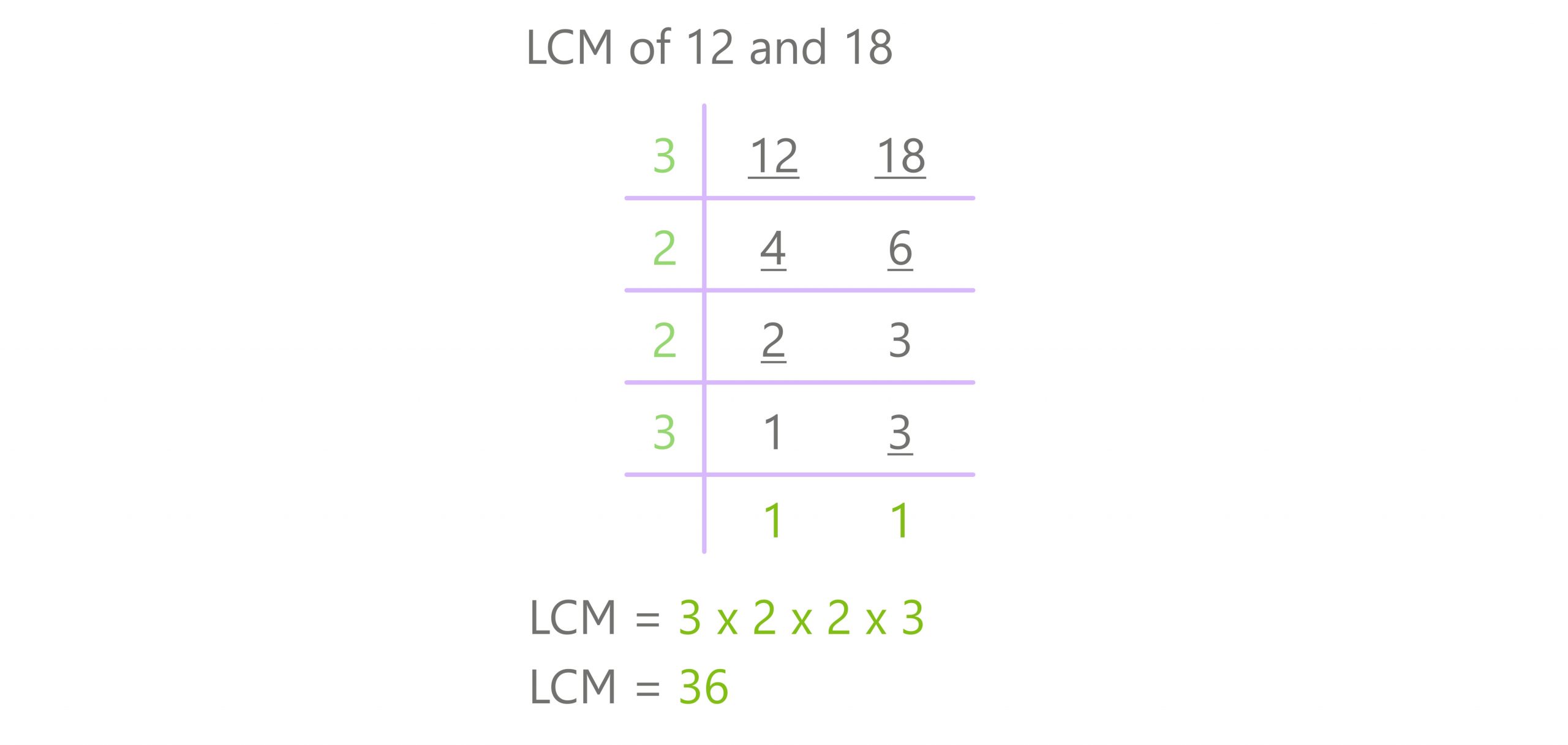
Climbing the Ladder: The Ladder Method

Now, here’s a method that’s both fun and effective: the ladder method. It’s like climbing a ladder, step by step, until you reach the top. In this case, the top is the LCM.

Here’s how it works:

1. Write the numbers (9, 12, and 18) side by side.
2. Find a common factor (like 3) and divide each number by it.
3. Keep dividing by common factors until there are no more.
4. Multiply all the factors you used to get the LCM.

Let’s do it together:

• 9 ÷ 3 = 3
• 12 ÷ 3 = 4
• 18 ÷ 3 = 6

Now, divide again:

• 3 ÷ 3 = 1
• 4 ÷ 2 = 2
• 6 ÷ 2 = 3

Multiply the factors: 3 × 3 × 2 × 2 = 36. Tada! We’ve got our LCM.

Why the Ladder Method Rocks

The ladder method is great because it’s visual and easy to follow. It’s like having a roadmap that guides you step by step to the solution. Plus, it’s super handy when you’re dealing with larger numbers.

Real-Life Applications of LCM

LCM isn’t just a math concept—it’s a real-life problem solver. Here are a few examples:

• Scheduling: If you’re coordinating events that happen at different intervals, LCM helps you find the next time they’ll coincide.
• Construction: Builders use LCM to ensure that materials align perfectly, especially when working with different units of measurement.
• Cooking: Need to adjust a recipe for a larger group? LCM helps you scale up ingredients without losing proportions.

See? LCM is everywhere!

Common Mistakes to Avoid

Even the best mathletes make mistakes sometimes. Here are a few pitfalls to watch out for:

• Forgetting to check for common factors: Always double-check that you’ve divided by all possible factors.
• Skipping steps: Take your time with each method. Rushing can lead to errors.
• Ignoring prime numbers: Prime factorization is your friend. Don’t overlook it!

Remember, practice makes perfect. The more you work with LCM, the better you’ll get at avoiding these mistakes.

Tips and Tricks for Mastering LCM

Ready to level up your LCM game? Here are a few tips to keep in mind:

• Start small: Practice with smaller numbers before tackling the big ones.
• Use visuals: Draw diagrams or use tools like the ladder method to make things clearer.
• Stay organized: Keep your work neat and tidy. It’ll help you spot mistakes and stay on track.

And don’t forget: it’s okay to ask for help. Whether it’s a teacher, a friend, or even an online resource, there’s no shame in seeking guidance.

Solved Examples: Putting It All Together

Let’s wrap things up with a few solved examples. These will help solidify your understanding of LCM.

Example 1: LCM of 6, 8, and 12

Using prime factorization:

• 6 = 2 × 3
• 8 = 2 × 2 × 2
• 12 = 2 × 2 × 3

Take the highest powers: 2 × 2 × 2 × 3 = 24. The LCM is 24.

Example 2: LCM of 15, 20, and 30

Using the list method:

• Multiples of 15: 15, 30, 45, 60, …
• Multiples of 20: 20, 40, 60, …
• Multiples of 30: 30, 60, …

The first common multiple is 60. The LCM is 60.

Conclusion: Your Math Journey Continues

And there you have it—the ultimate guide to mastering the LCM of 9, 12, and 18. Whether you’re using prime factorization, the list method, or the ladder method, you now have the tools to tackle any LCM problem that comes your way.

Remember, math isn’t just about numbers—it’s about problem-solving. And with LCM in your toolkit, you’re well on your way to becoming a math wizard. So, what are you waiting for? Go out there and conquer those math challenges!

Got questions? Leave a comment below, and let’s chat. And don’t forget to share this article with your friends. Knowledge is power, and sharing it makes us all stronger!